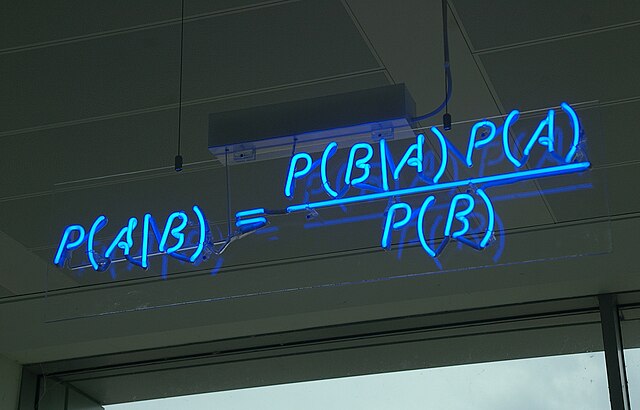Does a new study really identify genes that determine whether you’ll go to college? Um, no. Photo by velkr0.
Does a new study really identify genes that determine whether you’ll go to college? Um, no. Photo by velkr0.Identifying a genetic basis for human intelligence is fraught with huge ethical, social, and political implications. If we knew of gene variants that increased intelligence, would we try to engineer them into our children? Or use them to determine who gets college loans? Or maybe just discourage people carrying the wrong variant from having children? So you’d think that researchers working on that topic would proceed with extra caution, and make sure their conclusions were absolutely iron-clad before submitting results for publication in a scientfic journal—and that peer reviewers working for journals in that field would examine the work that much more closely before agreeing to publication.
Yeah, well, if you thought that, you would be wrong.
A paper just published online ahead of print at the journal Culture and Brain claims to have identified genetic markers that (1) differentiate college students from the general population and (2) are significantly associated with cognitive and behavioral traits. Cool, right? That would mean that these marker identify genes that determine whether you make it to college, and how well you do in educational settings generally—they’re genes that contribute to intelligence.
Again, if you thought that, you’d be wrong. But in that wrongness, you’re in good company, alongside the authors of this paper and, apparently, everyone involved in its peer review and publication.
Here’s what the paper’s authors did to identify these “intelligence” genes. They recruited almost 500 students at Beijing Normal University, took blood samples from them, and gave them all a series of 49 different cognitive and behavioral tests, covering problem solving, memory, language and mathematical ability, and a bunch of other things we generally think of as having to do with intelligence. Using the blood samples, the authors genotyped all of the students at 284 single-nucleotide polymorphism (SNP) markers located in genes with expected connections to brain function—either because they’re involved in producing neurotransmitters, or they’re strongly expressed in the brain.
Next, the authors tested each of the 284 SNPs for deviation from Hardy-Weinberg Equilibrium, or HWE. If you’re not familiar with the concept, here’s my attempt at a brief explanation: HWE boils down to probability.
We all carry two complete sets of genes—one from Dad, one from Mom. So, suppose there’s a spot in the genome where two possible variants—let’s call them A and T—can occur. This is exactly what a SNP is, a single letter of DNA code that differs from person to person. Taking into account the two copies of eaach gene we carry, every person can have one of three possible diploid genotypes at that single-letter spot: AA, AT, or TT.
If we know how common As and Ts are in the population as a whole, we can estimate how common those three diploid genotypes should be: the frequency of the first allele times the frequency of the second allele. Say you’ve genotyped a sample of people, and you find that 40% of the markers are As (a frequency of 0.4), and 60% are Ts (frequency of 0.6). Then, if the two variants are distributed randomly among all the people you’ve sampled, you’d expect to find 16% (0.4 × 0.4 = 0.16) AA genotypes, 36% (0.6 × 0.6 = 0.36) TT genotypes, and 48% either AT or TA genotypes (0.4 × 0.6 + 0.6 × 0.4 = 0.48).
If the actual frequencies of the three genotypes are close to that expectation, we say the SNP is in Hardy-Weinberg equilibrium, a state named for the two guys who originally deduced all this. Deviations from HWE may occur if, for some reason, people are more likely to mate with people who carry the same genotype, or if the three possible genotypes are associated with having different numbers of children—different fitness, in the evolutionary sense. So a deviation from HWE may mean something is going on at the deviating spot in the genome.
Of the 284 SNPs, the authors identified 24 with genotype frequecies that show a statistically significant deviation from HWE—in their sample of college students, that is. They also examined HWE for the same SNPs in a sample taken from the general population of Beijing, as part of the 1000 Genomes database of human genetic diversity, and found that all but 2 of the 24 SNPs that violated HWE in the students were within HWE expectations in the comparison sample. They conclude that this means that something about these 24 SNPs sets the college students apart from the broader population of Beijing.
Except this is not how population geneticists calculate genetic differentiation between two groups of people. For that, we usually use a statistic called FST, which essentially calculates the degree to which allele frequencies differ between two groups. That is, if the students are really differentiated from the rest of Beijing at a particular SNP, then we’d expect the frequency of the A allele among the students to be really different from the frequency of A in the other sample. FST is related to deviation from HWE; but it’s not at all the same thing. Fortunately for us all, the authors published all their genotype frequency data as Tables 1 and 2 of the paper. I can check directly to see whether the FST at each locus suggests meaningful genetic differentiation between the students and the comparison sample.
 The distribution of FST values calculated from the 24 SNPs. Image by jby.
The distribution of FST values calculated from the 24 SNPs. Image by jby.Possible values for FST range from 0, when there is no difference between the two groups being compared; and 1, when the two groups are completely differentiated. The FST values I calculated from the data tables range from 0.00003 to 0.05432, and half of them are less than 0.002—that’s within the range seen for any random sample of genetic markers in other human populations [PDF]. Which is to say, the 24 SNPs identified in this paper are not really that differentiated at all.
Uncorrected testing is un-correct
But these markers identified in the study are still associated with congnitive ability, right? Well, brace yourself: there are serious problems with that claim, too. To test for association with cognition, the authors conducted a statistical test asking whether students with each of the three possible genotypes at a given SNP differed in the scores they got on the different cognitive tests. If the difference among genotypes was greater than expected by chance, they concluded that the SNP was associated with the element of intelligence approximated by that particular cognitive test. They identified these “significant” associations using a p-value cutoff of 0.01, which is a technical way of saying that the probability of observing the difference among genotypes simply by chance is less than 1 in 100.
The authors tested for associations of the genotypes at 19 SNPs (excluding 5 that would’ve had too few people with one or more of the three genotypes) with all 49 cognitive tests. They conducted each test using the complete sample of students, and then also the males and females separately, in case there were gender differences in the effects of each SNP. Across all three data sets (total, male, and female), they found 17 significant associations.
Statisticians and regular readers of xkcd will probably already know where this is going.
If you conduct one statistical test using a particular dataset, and see that there’s a 1 in 100 chance of observing the result purely by chance, you can be reasonably sure (99% sure!) that your result isn’t due to chance. However, if you conduct 100 such tests, and only one of them has a p-value of 0.01, then that is quite possibly the one time in 100 the result is pure coincidence. Think of it this way: it’s a safe bet that one roll of a die won’t be a six; but it’s not such a safe bet that if you roll a die six times, you won’t roll a six at least once. In statistics, this is called a multiple testing (or multiple comparisons) problem.
How many tests did the authors conduct? That would be 49 cognitive measurements × 19 SNPs, or 931 tests on each of the three separate datasets. At p = 0.01, you’d expect them to get somewhat more than 9 “significant” results that aren’t actually significant. And, indeed, for the total datset, they found 7 significant results; for the male students alone, they found 3; and for the females, 7. That’s exactly what would happen if there were no true associations between the SNP genotypes and the cognitive test results at all.
And, to go all the way back to the beginning, what was the p-value cutoff for the authors’ test of HWE? They considered deviations from HWE significant if the probability of observing the deviation by chance was less than 5%, or p ≤ 0.05. And 5% of 284 SNPs is a bit more than 14. That’s a pretty big chunk of their 24-SNP list.
In short, the authors of this paper identified a list of SNPs that supposedly differentiate college students from the general population, using a method that doesn’t actually identify differentiated SNPs. They then conducted a series of tests for association between those SNPs and intelligence-related traits, and didn’t find any more association than expected purely by chance. The list of genes identified this way is literally no better than what you’d get using two spins of a random number generator.
Who cares about methodological correctness, anyway?
What really makes me angry about this paper, though, is this: there are ways to do it right. The authors could have talked to a population geneticist, who would have told them to use FST or a similar measure of genetic differentiation. They could have used any number of methods to correct for the multiple testing problem in their final test for associations. And, in fact, someone must have pointed that second one out to them, because here’s what they write in the final paragraph of the paper:
… we analyzed all significant main effects at the P ≤ 0.01 level, without using more stringent corrections for multiple comparisons. We deemed this as an exploratory study to see if there were any behavioral or cognitive correlates of the SNPs in HWD. These results should provide bases for future confirmatory hypothesis-testing research.
In other words, they’re just fishing around for genes, here, so why should they actually perform a statistically rigorous test? But precisely because they don’t correct for multiple testing, any money spent on “future confirmatory hypothesis-testing research” would be wasted—it might as well start with a random selection of SNPs from the original list the authors chose to examine.
Given the nature of its subject matter, it’s appalling to me that this paper made it through peer review and into a scientific journal. It certainly wouldn’t have made it into a journal whose editors and reviewers understood basic population genetics. If I had to guess, I’d speculate that Culture and Brain doesn’t have any geneticists in its reviewer rolls—the fact that the authors spend a large chunk of their Introduction simply explaining Hardy-Weinberg Equilibrium suggests that their audience is people who don’t know much about the kind of data being presented.
And that’s where we come to the real lesson of this study. It’s getting cheaper and easier to collect genetic data with every passing day—to the point that researchers with no prior expertise or experience with genetic data can now do it. I’m afraid we’re going to see a lot more papers like this one, in the years to come.◼
Reference
Chen C., Chen C., Moyzis R.K., He Q., Lei X., Li J., Zhu B., Xue G. & Dong Q. Genotypes over-represented among college students are linked to better cognitive abilities and socioemotional adjustment, Culture and Brain, DOI: 10.1007/s40167-013-0003-3
Clark A.G., Nielsen R., Signorovitch J., Matise T.C., Glanowski S., Heil J., Winn-Deen E.S., Holden A.L. & Lai E. (2003). Linkage disequilibrium and inference of ancestral recombination in 538 single-nucleotide polymorphism clusters across the human genome, The American Journal of Human Genetics, 73 (2) 285-300. DOI: 10.1086/377138